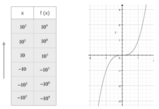
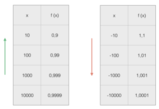
Limite di una funzione
Calcolare il limite di una funzione per[math]x[/math]
che si avvicina ad un determinato valore significa calcolare il valore che la funzione [math]y=f(x)[/math]
assume quando la [math]x[/math]
si appresta ad assumere il valore stabilito. In altre parole: il limite permette di studiare una funzione anche laddove non sia definita nel suo dominio. Si parla di punti di discontinuità, di non esistenza, in cui si vuole comprendere come la funzione si comporti in prossimità di queste situazioni.In termini matematici un limite di una funzione viene definito come segue:
[math]\lim_{x\to x_0}[f(x)][/math]
Esistono diverse definizioni di limite:
- Limite finito che tende ad un valore finito
- Limite finito che tende ad un valore infinito
- Limite infinito che tende ad un valore finito
- Limite infinito che tende ad un valore infinito
Gli intorni
Quando si introduce il concetto di limite si introduce anche il concetto di intorno di un punto.Un intorno è un intervallo formato da tutti i numeri reali che soddisfano la disequazione:
[math]x_0–\delta>x>x_0+\delta[/math]
Gli intorni possono essere destri di
[math]x_0[/math]
se:
[math]x_0>x>x_0+\delta[/math]
L'intorno destro sarà il mezzo attraverso cui si definirà il limite destro.
Gli intorni possono essere sinistri di
[math]x_0[/math]
se:
[math]x_0-\delta>x> x_0[/math]
L'intorno destro sarà il mezzo attraverso cui si definirà il limite sinistro.
Limite finito che tende ad un valore finito
Il limite finito per[math]x[/math]
che tende ad un numero finito viene definito come segue. Sia data una funzione [math]y = f(x)[/math]
si dice che essa ha limite finito ([math]l[/math]
) per [math]x[/math]
che tende ad [math]x_0[/math]
finito se, preso a piacere una quantità positiva e piccolissima [math]\varepsilon[/math]
è possibile determinare in corrispondenza di esso un intorno completo di [math]x_0[/math]
che appartiene all’insieme di definizione della funzione tale che per ogni [math]x[/math]
di questo intorno risulti:
[math]l – \varepsilon > f(x) > l + \varepsilon[/math]
Limite infinito che tende ad un valore finito
Limite infinito per[math]x[/math]
che tende ad un numero finito viene definito come segue. Si dice che una funzione [math]f(x)[/math]
ha limite infinito per [math]x[/math]
che tende ad un numero finito [math]x_0[/math]
se, fissato un numero [math]M[/math]
grandissimo a piacere è possibile determinare in corrispondenza di esso un intorno completo di [math]x_0[/math]
contenuto nell’insieme di definizione della funzione.
Limite finito che tende ad un valore infinito
Limite finito per[math]x[/math]
che tende ad infinito viene definito come segue. Si dice che una funzione [math]y= f(x)[/math]
ha limite finito ([math]l[/math]
) per [math]x[/math]
che tende ad infinito se, presa una quantità [math]\varepsilon[/math]
piccola positiva è possibile determinare in corrispondenza di essa un intorno di + infinito o un intorno di – infinito contenuto nell’insieme di definizione della funzione tale che per ogni [math]x[/math]
di questo intorno si abbia :[math]l – \varepsilon > f(x) > l + \varepsilon[/math]
Limite infinito che tende ad un valore infinito
Limite infinito per[math]x[/math]
che tende ad un numero infinito viene definito come segue. Si dice che una funzione [math]f(x)[/math]
tende ad infinito per [math]x[/math]
che tende ad un numero finito [math]x_0[/math]
se, fissato un numero [math]M[/math]
grandissimo a piacere è possibile determinare in corrispondenza di esso un intorno completo di [math]x_0[/math]
contenuto nell’insieme di definizione della funzione.
Algebra dei limiti
Siano dati i seguenti limiti:
[math]\lim_{x\to x_0}[f(x)]=l[/math]
[math]\lim_{x\to x_0}[g(x)]=m[/math]
Il limite della somma tra le funzioni
[math]f(x[/math]
e [math]g(x)[/math]
sarà sarà:
[math]\lim_{x\to x_0}[f(x)+g(x)]=l+m[/math]
Ovvero il limite della somma tra due funzioni sarà la somma dei singoli valori dei limiti calcolati.
Il limite della differenza tra le funzioni
[math]f(x[/math]
e [math]g(x)[/math]
sarà:
[math]\lim_{x\to x_0}[f(x)-g(x)]=l-m[/math]
Ovvero il limite della differenza tra due funzioni sarà la differenza dei singoli valori dei limiti calcolati.
Il limite del quoziente tra le funzioni
[math]f(x[/math]
e [math]g(x)[/math]
sarà:
[math]\lim_{x\to x_0}[\frac{f(x)}{g(x))}]=\frac{l}{m}[/math]
Ovvero il limite del quoziente tra due funzioni sarà il quoziente dei singoli valori dei limiti calcolati.
Il limite del prodotto tra le funzioni
[math]f(x[/math]
e [math]g(x)[/math]
sarà:
[math]\lim_{x\to x_0}[f(x)\cdot g(x)]=l\cdot m[/math]
Ovvero il limite del prodotto tra due funzioni sarà il prodotto dei singoli valori dei limiti calcolati.
Il limite del prodotto tra la funzione
[math]f(x[/math]
e una costante sarà:
[math]\lim_{x\to x_0}[k\cdot g(x)]=k\cdot m[/math]
Ovvero il limite del prodotto tra una funzione e una costante sarà il prodotto tra la costante e il limite calcolato.
Il limite della funzione
[math]f(x[/math]
elevata ad una potenza generica sarà:[math]\lim_{x\to x_0}[{f(x)^{\frac{m}{n}}}]=l^{\frac{m}{n}}[/math]
Ovvero il limite della funzione elevata ad una potenza generica sarà il valore del limite calcolato elevato alla potenza generica.
Teorema dell'unicità del limite
Se una funzione[math]f(x)[/math]
ammette un limite per [math]x[/math]
che tende ad [math]x_0[/math]
tale limite è unico.Questo teorema vale sempre.
Teorema della permanenza del segno
Se per[math]x[/math]
che tende ad [math]x_0[/math]
la funzione [math]f(x)[/math]
ha per limite un numero finito diverso da [math]0[/math]
esiste un intorno di [math]x_0[/math]
tale che per ogni [math]x[/math]
la funzione assume valori dello stesso segno del limite.
Punti di discontinuità
Se una funzione non è continua in un punto[math]x_0[/math]
tale punto è detto di discontinuità, esistono punti di discontinuità di prima seconda e terza specie. Quelli di prima specie si hanno quando nel punto [math]x_0[/math]
il limite destro e sinistro esistono ma sono diversi. Quelli di seconda specie se nel punto [math]x_0[/math]
non esiste o non è finito uno dei 2 limiti destro o sinistro. Quelli di terza specie si ha quando il limite finito esiste ma non esiste [math]f(x_0)[/math]
.
